Angle de vision
d'un réseau lenticulaire (anglais: lenticular):
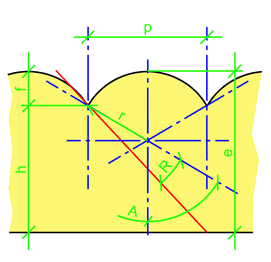
Données
calculées:
L'angle de réfraction
R correspond à l'angle
formé par la droite partant
de
l'axe de la lenticule jusqu'a une extrémité ou bord de
lenticule et de la droite partant de ce même point jusqu'a
l'opposé de la fin de séquence d'impression du pitch
concerné.
Pour calculer cette
première droite; il faut déterminer l'hauteur
h
du support à
l'un des bords de la lenticule. Il correspond à l'épaisseur
e
du support moins la flèche
f
de l'arc de la lenticule.
La flèche
f
est égale au
rayon
r
de la lenticule moins la racine carré du carré du même
rayon moins le carré de la moitié du pitch
p
soit
f
=
r
-
√
r2 - (p/2)2)
Soit
f
=
190,5µ - √
((190,5 * 190,5) - ((336,65/2) * (336,65/2)) =
101,3µ.
Hauteur du
support à une extrémité de lenticule
h =
Épaisseur
e - Flèche
f
Soit 457µ -
101,3µ = 355,7µ
Maintenant, il
nous faut calculer l'angle A
formé par le demi arc de la lenticule.
Il est égale à l'angle du sinus du pitch
p
sur
deux divisé par le rayon
r
soit égale sin ((p/2)
/
r)
Soit sin = (336,65/2) /
190,5 = 0,883 soit un angle de 62,08°.
L'angle de
réfraction
R
est égale à cette angle (62°) moins l'angle de la tangente
du pitch sur notre hauteur h précédemment calculée soit tan
= 336,65 /
355,7 =
0,946 soit un angle 43,42° soit 62,08° - 43,42° = 18,65°.
|



